用 A* Search Algorithm 走迷宮

發表於 分類於 閱讀次數： 文章字數： 782 所需閱讀時間 ≈ 3 分鐘

前言

前一篇文章中，我使用了 Eller’s Algorithm 迷宮生成算法 來生成迷宮，這一篇文章會先介紹 A* Algorithm，並使用 A* Search Algorithm 來攻略迷宮，先偷看一下成果:
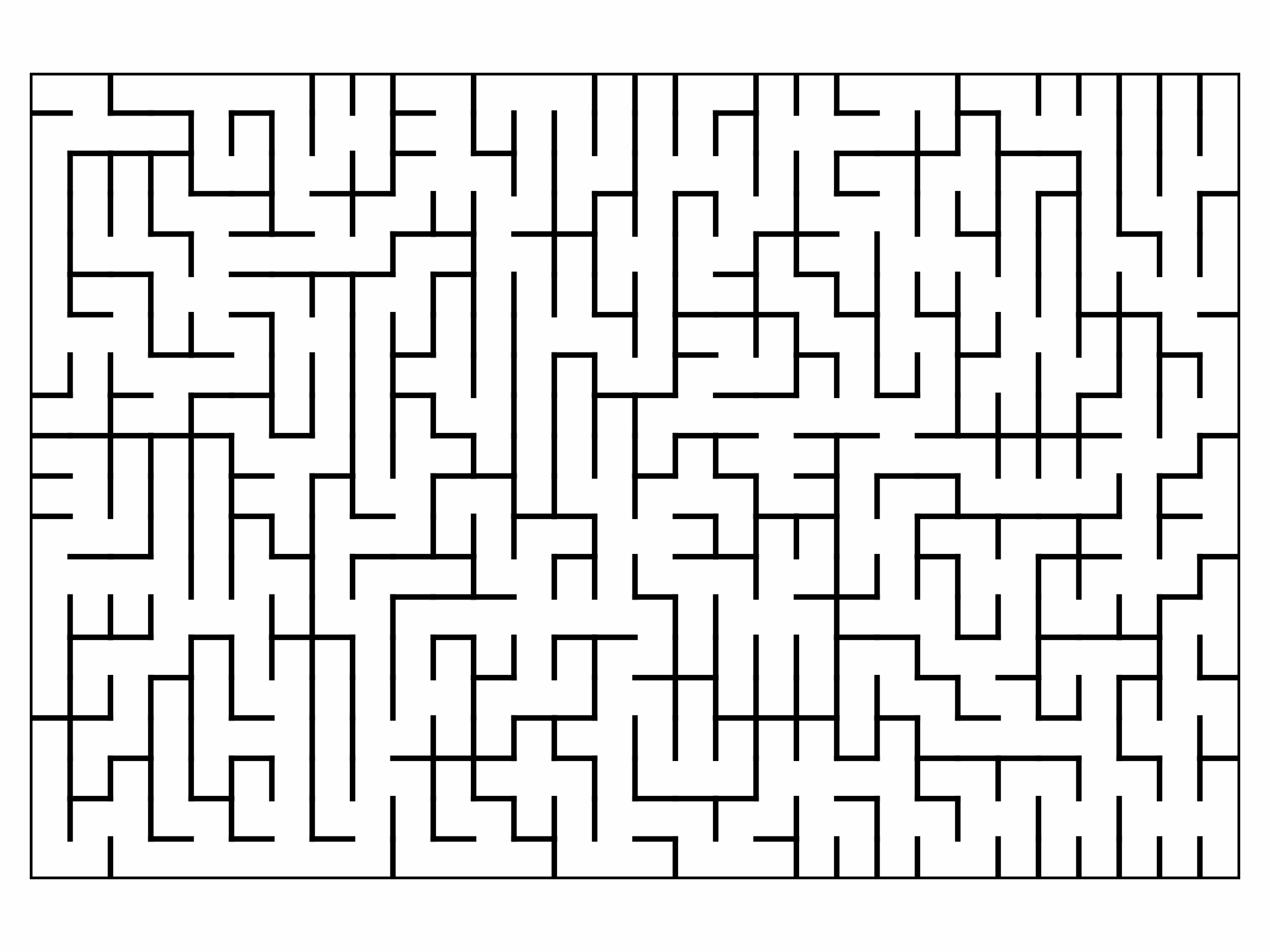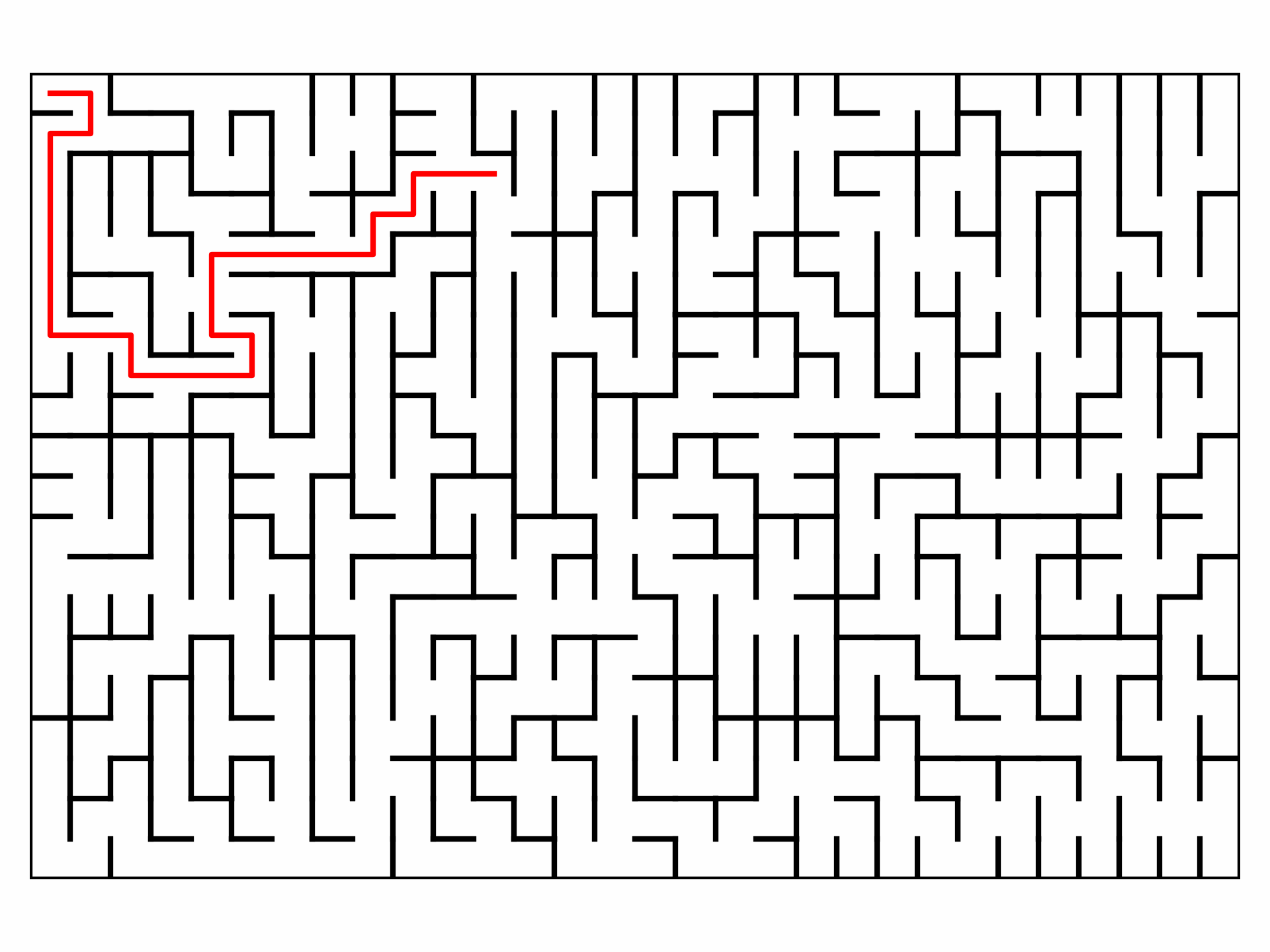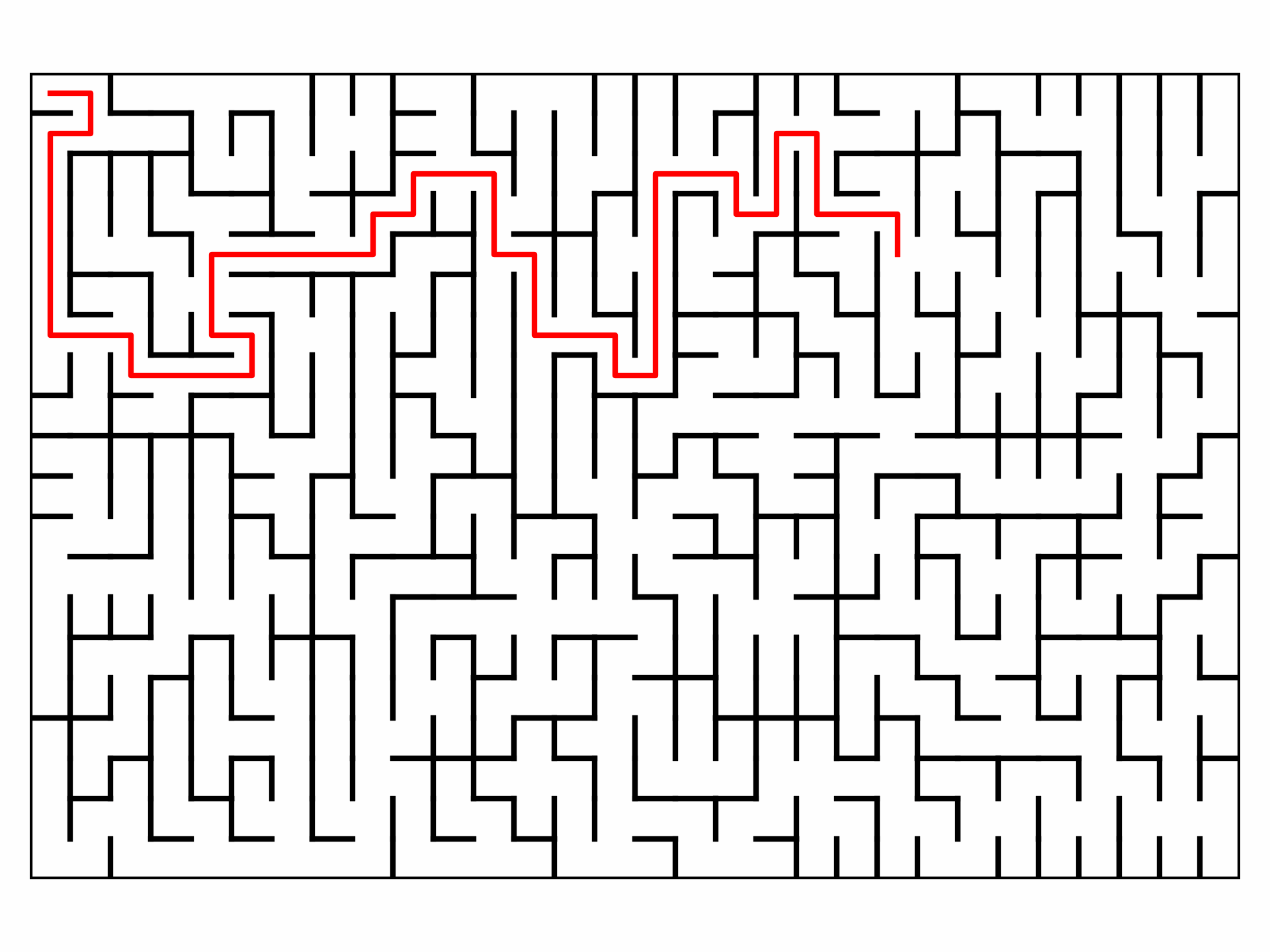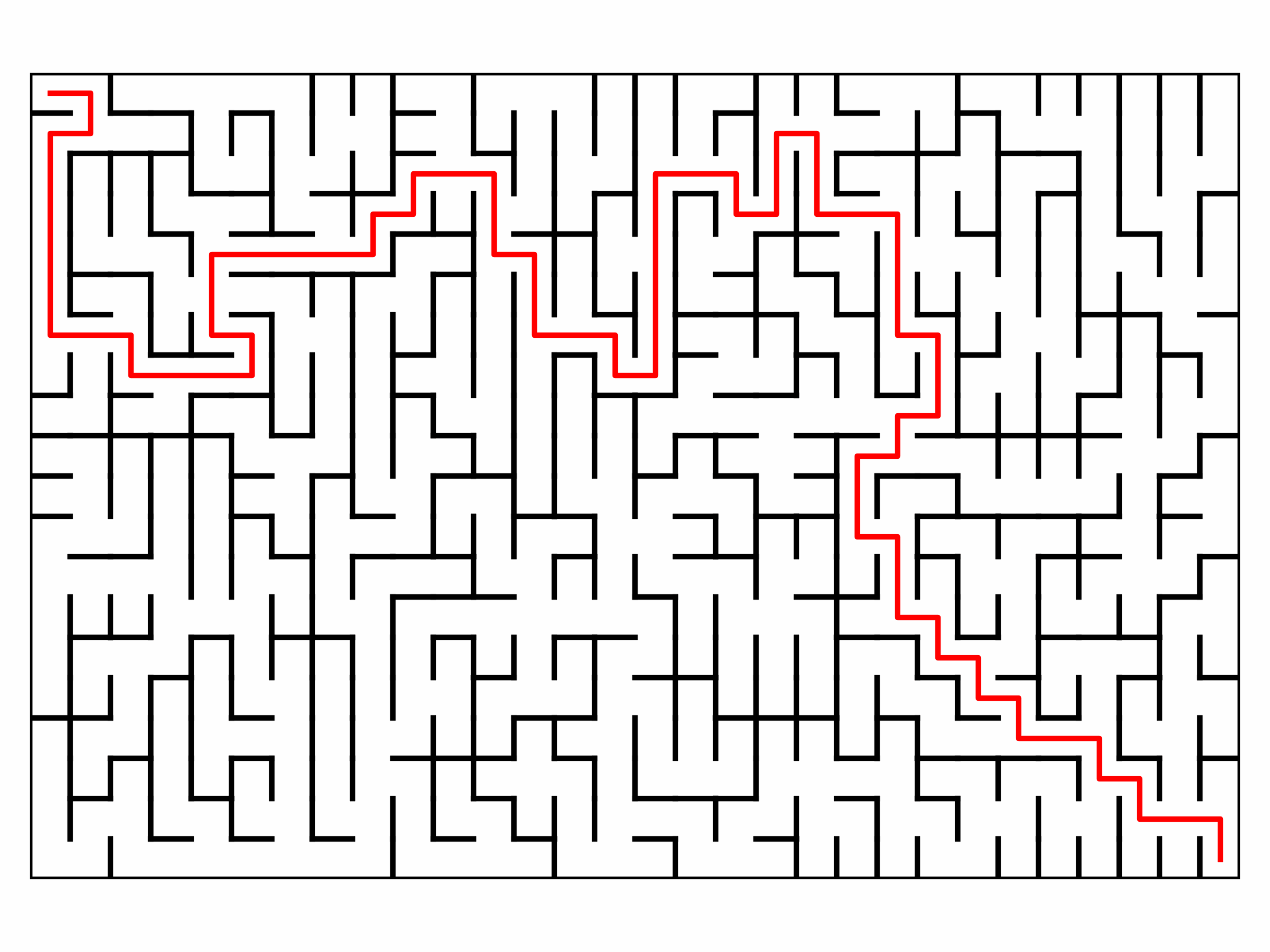
maze_animation

A* Search Algorithm

A* 是一種最短路徑算法，它跟 Dijkstra 非常地相似，都會根據某個優先序來選擇下一步要走的路徑，唯一不同的點是 Dijkstra 的優先序只考量了目前「已走的距離」，因此它的搜尋方向會朝四周發散。但我們在搜尋路徑時通常會是有目的地，也就是知道方向的，一般情況下，我們不會想往反方向尋找最短路徑，所以 A* 在 Dijkstra 的基礎上多考慮了未來「預期要走的距離」。

簡單地去理解，「已走的距離」+「預期要走的距離」基本上就會是整趟路的距離，而直接用整趟路的距離來排序優線序，大部分情況下都能幫助我們更快找到最短路徑，這取決於我們對預期的估算是否準確。不過也不用想得太複雜，對於這個預期，通常直接用簡單的距離函式求得就好，如歐幾里德距離或曼哈頓距離。

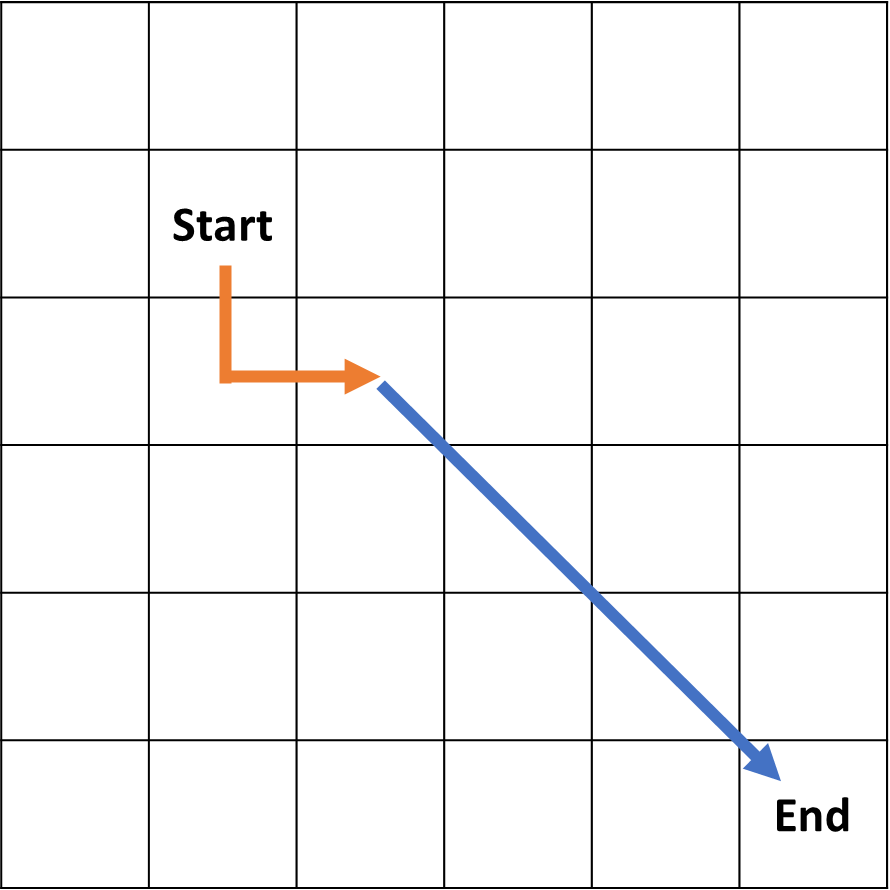
以下圖來說，橘色是已走的距離，Dijkstra 只會考慮這一段，藍色則是預期要走的距離，橘色+藍色就是 A* 會考慮的範圍。

distance

Python 實現

不能說跟 Dijkstra 很像，基本上是一模一樣，只是把 priority queue 裡面內容換成整趟路的距離。

搜索路徑

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
import heapq

def future_cost(y, x, target_y, target_x):
    return abs(y-target_y) + abs(x-target_x)

def barrier(graph, y, x, i, j):
    if i == 1:
        return graph[y][x] & 2
    if j == 1:
        return graph[y][x] & 1
    if i == -1:
        return graph[y-1][x] & 2
    return graph[y][x-1] & 1

def a_star(graph, start_y, start_x, target_y, target_x):

    n = len(graph)
    m = len(graph[0])
    ways = [(0, 1), (1, 0), (0, -1), (-1, 0)]

    min_cost = [[float('inf')]*m for _ in range(n)]
    min_cost[start_y][start_x] = 0

    prev = [[None]*m for _ in range(n)]
    heap = [(0, 0, start_y, start_x)]

    # find path, update distance
    while heap:
        _, past_cost, y, x = heapq.heappop(heap)

        if y==target_y and x==target_x:
            break
        
        past_cost += 1
        for i, j in ways:
            nxt_y = y+i
            nxt_x = x+j
            if nxt_y<0 or nxt_x<0 or nxt_y==n or nxt_x==m:
                continue
            if barrier(graph, y, x, i, j):
                continue

            if past_cost < min_cost[nxt_y][nxt_x]:
                min_cost[nxt_y][nxt_x] = past_cost
                prev[nxt_y][nxt_x] = (y, x)
                tot_cost = future_cost(nxt_y, nxt_x, target_x, target_y) + past_cost
                heapq.heappush(heap, (tot_cost, past_cost, nxt_y, nxt_x))


    # construct path
    curr_y = target_y
    curr_x = target_x
    path = [(curr_y, curr_x)]
    while prev[curr_y][curr_x] != None:
        curr_y, curr_x = prev[curr_y][curr_x]
        path.append((curr_y, curr_x))
    path.reverse()

    return path

繪製路徑

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import matplotlib.pyplot as plt
import matplotlib.animation as animation

def plot_path(maze, path, fig, ax):
    height = len(maze)

    # 初始化函數
    adjusted_path = [(x+0.5, height-y-0.5) for y, x in path]
    x_data, y_data = zip(*adjusted_path)

    def init():
        line.set_data([], [])
        return line,

    # 更新函數
    def update(num):
        line.set_data(x_data[:num+1], y_data[:num+1])
        return line,

    line, = ax.plot([], [], 'r', lw=2)
    ani = animation.FuncAnimation(fig, update, frames=len(path), init_func=init,
                                interval=100, blit=True, repeat=False)
    
    return fig, ax, ani

執行結果

1
2
3
4
5
6
7
8
9
10
11
12
height = 20
width = 30

# maze (code in prev article)
maze = ellers_algorithm(height, width)
fig, ax = plot_maze(maze)

# path
path = a_star(maze, 0, 0, height-1, width-1)
fig, ax, ani = plot_path(maze, path, fig, ax)
plt.tight_layout()
plt.show()

成果如下:
maze_animation