資料結構筆記 - 布隆過濾器 Bloom Filter

發表於 分類於 閱讀次數： 文章字數： 682 所需閱讀時間 ≈ 3 分鐘

bloom-filter

Summary

  • 用途: 用來快速判斷元素是否存在於一個集合中
  • 優點: 快速、節省空間
  • 缺點: 可能有 false positive (不存在但判定為存在)
  • 應用:
    • Check Duplicate: name、email 等是否已被使用
    • Filters: 過濾惡意請求 (ex: Cache penetration)、垃圾郵件等

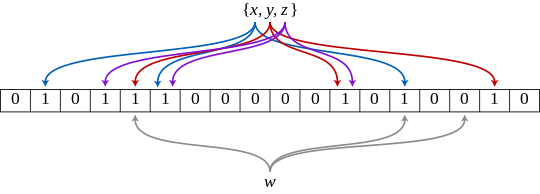
原理

對元素使用 k 個 Hash Functions，將其映射到長度為 m 的 Array 中，寫入時將映射到的 k 個位置標示為 1，檢查時如果映射到的 k 個位置都命中，表示該元素可能存在。

  1. 由預期的 False positive rate (p) 以及存入的資料筆數 (n) 來求出 Array Size (m) 以及 Hash Functions數 (k)

    • False positive rate
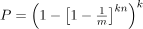
      false-positive-probability
    • Array size
      array-size
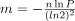
    • Number of hash functions
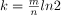
      number-of-hash-functions

  2. 選擇 Hash function
    可以使用 Non-Cryptographic Hash (非密碼雜湊函數)，雖然有 collision 的可能，但足夠好了，而且比較快。
    例如: MurmurHash、FarmHash、SpookyHash

實作

非原創! 基本上是下面參考文章中的程式碼，寫的很不錯所以只有小小修改一下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
# Python 3 program to build Bloom Filter 
# Install mmh3 and bitarray 3rd party module first 
# pip install mmh3 
# pip install bitarray 
import math 
import mmh3 
from bitarray import bitarray 


class BloomFilter(object): 

	''' 
	Class for Bloom filter, using murmur3 hash function 
	'''

	def __init__(self, items_count, fp_prob): 
		''' 
		items_count : int 
			Number of items expected to be stored in bloom filter 
		fp_prob : float 
			False Positive probability in decimal 
		'''
		# False possible probability in decimal 
		self.fp_prob = fp_prob 

		# Size of bit array to use 
		self.size = self.get_size(items_count, fp_prob) 

		# number of hash functions to use 
		self.hash_count = self.get_hash_count(self.size, items_count) 

		# Bit array of given size, default all 0 
		self.bit_array = bitarray(self.size) 


	def add(self, item): 
		''' 
		Add an item in the filter 
		'''
		digests = [] 
		for i in range(self.hash_count): 

			# create digest for given item. 
			# i work as seed to mmh3.hash() function 
			# With different seed, digest created is different 
			digest = mmh3.hash(item, i) % self.size 
			digests.append(digest) 

			# set the bit True in bit_array 
			self.bit_array[digest] = True

	def check(self, item): 
		''' 
		Check for existence of an item in filter 
		'''
		for i in range(self.hash_count): 
			digest = mmh3.hash(item, i) % self.size 
			if self.bit_array[digest] == False: 

				# if any of bit is False then,its not present 
				# in filter 
				# else there is probability that it exist 
				return False
		return True

	@staticmethod
	def get_size(n, p): 
		''' 
		Return the size of bit array(m) to used using 
		following formula 
		m = -(n * lg(p)) / (lg(2)^2) 
		n : int 
			number of items expected to be stored in filter 
		p : float 
			False Positive probability in decimal 
		'''
		m = -(n * math.log(p))/(math.log(2)**2) 
		return int(m) 

	@staticmethod
	def get_hash_count(m, n): 
		''' 
		Return the hash function(k) to be used using 
		following formula 
		k = (m/n) * lg(2) 

		m : int 
			size of bit array 
		n : int 
			number of items expected to be stored in filter 
		'''
		k = (m/n) * math.log(2) 
		return int(k)

看一下成果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
n = 100000 # Number of items to add 
p = 0.05 # False positive probability 
  
bloomf = BloomFilter(n,p) 
print("Array size: {}".format(bloomf.size)) 
print("Number of hash functions: {}".format(bloomf.hash_count)) 
print("False positive probability: {}".format(bloomf.fp_prob)) 

# Add items
for i in range(n):
	bloomf.add(str(i))

# Check false positive rate on Test data
fp = 0
for i in range(n, 2*n):
	if bloomf.check(str(i)):
		fp += 1
print("False positive rate on test data: {:.4f}".format(fp/n))

可以看到實際的 FP Rate 與我們設定的非常接近。
filter-result

參考文章

Bloom Filters – Introduction and Implementation