Eller's Algorithm 迷宮生成算法
Eller’s Algorithm 算法介紹
Eller’s Algorithm 是一種神奇動態迷宮生成算法,可以在線性時間內逐行生成迷宮,用我自己的理解來說,算法的精神就是:
每個格子一開始都是被分隔開的「區域」,隨機打通格子間的牆壁使區域間可以相通。
步驟拆解
Eller’s Algorithm 大致上可以拆解為以下幾個步驟:
- 初始化第一行
每個格子都有一個唯一的區域編號,彼此之間都是分隔的。

- 橫向連接
隨機打通相鄰格子之間的橫向牆壁,將它們合併到同一個區域中。

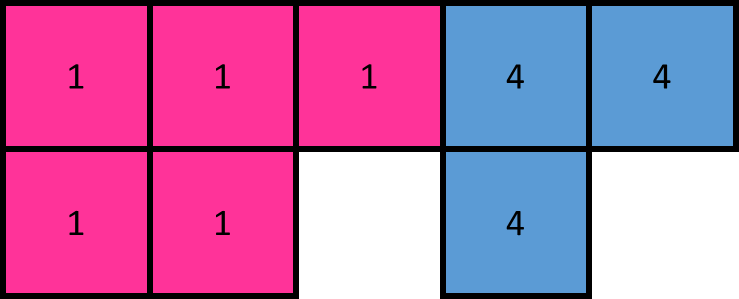
- 垂直連接
每個區域至少有一個格子向下連接,確保迷宮在下一行是連通的。
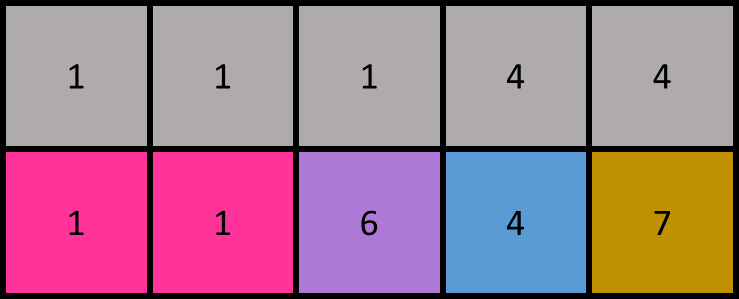
- 新增區域
分配新的區域編號給尚未連接的格子,由於算法只關注最新的一行,所以前面的幾行都不用管了。
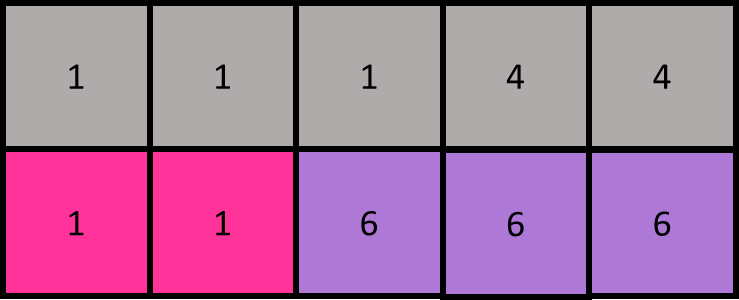
- 迭代生成
重複 2~4 的步驟


- 處理最後一行
確保最後一行所有格子都連接 (打通所有區域),以形成一個完整的迷宮。
ps. 連通的是區域,不代表最後一列沒有橫向的牆壁
Python 實現
雖然說算法邏輯是打通區域,但區域是個抽象的概念,實際上程式寫起來會比較像在各個格子間「建牆」。
生成迷宮
1 | import random |
繪製迷宮
1 | import matplotlib.pyplot as plt |
執行結果
1 | height = 20 |
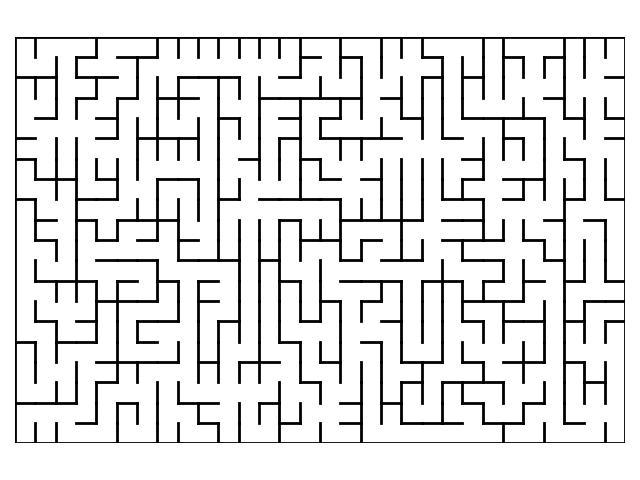
成果如下:

預告
下一篇文章用 A* 算法走迷宮 ~