Monotonic Stack

發表於 分類於 閱讀次數： 文章字數： 743 所需閱讀時間 ≈ 3 分鐘

Monotonic Stack 本質上就是一個 Stack 而已，只不過在操作 Stack 時需要同時維護其單調的特性，本文會簡單介紹 Monotonic Stack 並附上兩個有一點點難度的 LeetCode 題目做練習：84. Largest Rectangle in Histogram、85. Maximal Rectangle。

Usage

白話來說，如果我們要維護一個單調遞增的 stack (如上圖)，那麼在 push 新元素時要先和 stack 的 top 進行比較，如果新的元素比較大就直接放進去，如果新的元素比較小的話，就要先將 stack 中大於新元素的元素依次 pop 出來，之後才放入新元素，如此一來便能維護 Stack 的單調性。

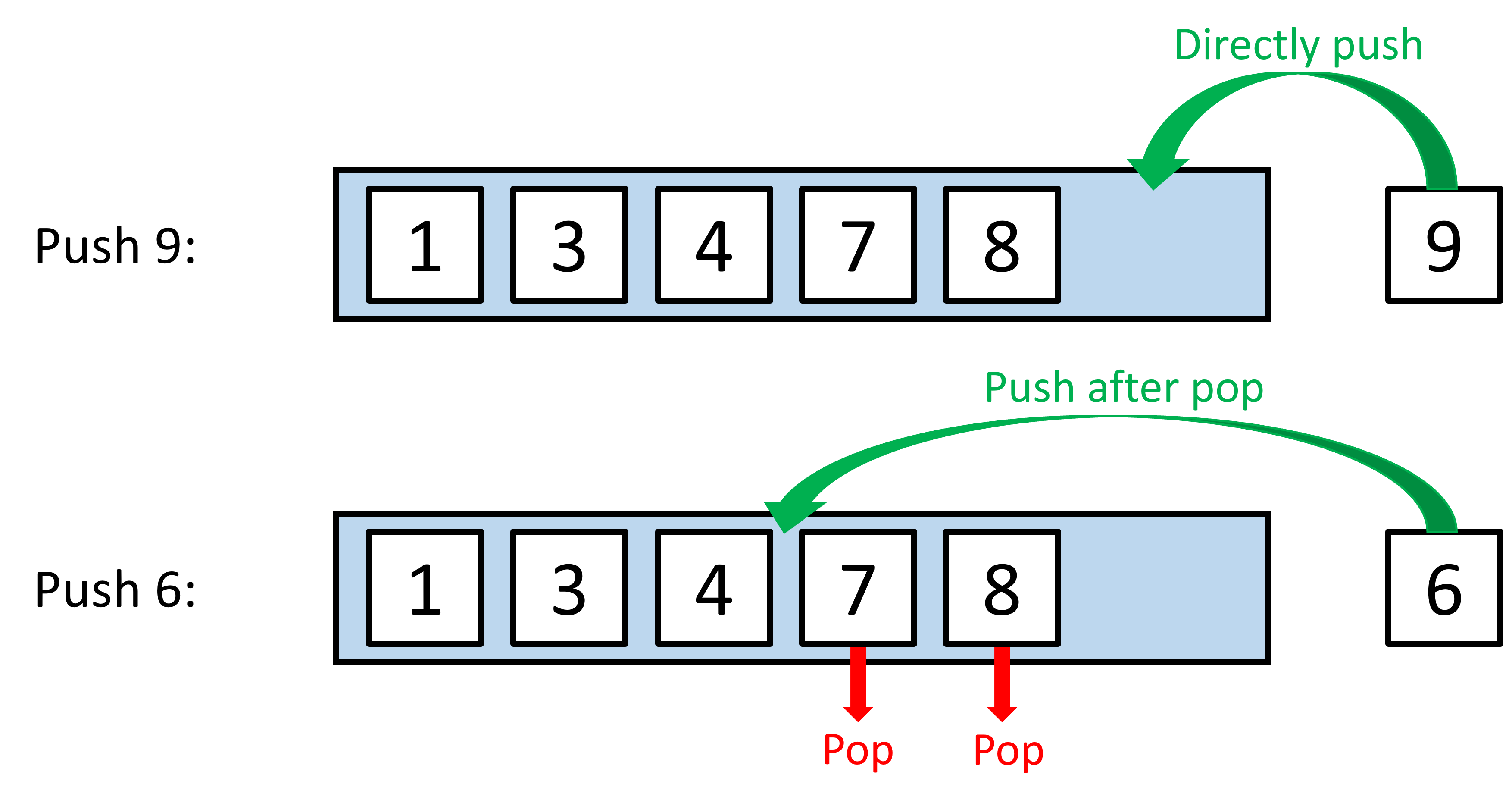
monotonic stack

依此類推，單調遞減也是差不多作法。

LeetCode Example

84. Largest Rectangle in Histogram

Largest Rectangle in Histogram

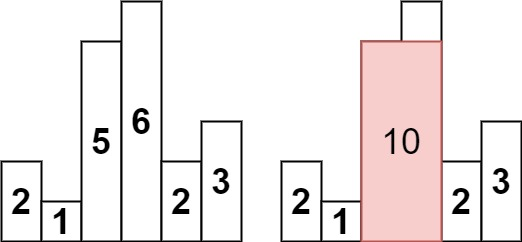
在這個題目中，我們要找出直方圖所能組成的最大長方形面積，我們其實可以把它看作 Next Smaller Element 問題的變形，找到對於每個 hist 來說，下一個比它低的 hist 在哪，如此便能的到它長方形的寬，進一步計算出長方形的面積。
具體來說，我們在遍歷直方圖的同時維護一個 Monotonic Stack，每次 pop 時都去計算被 pop 掉的柱體最多可以組成多少面積，以上圖來說：

  • push 2
    直接放入 2，stack = [2]
  • push 1
    1 < 2，pop 2，長方形面積為 2 * 1 = 2。
    放入 1，stack = [1]
  • push 5
    直接放入 5，stack = [1, 5]
  • push 6
    直接放入 6，stack = [1, 5, 6]
  • push 2
    2 < 6，pop 6，長方形面積為 6 * 1 = 6。
    2 < 5，pop 5，長方形面積為 5 * 2 = 10。
    放入 2，stack = [1, 2]
  • …

下面的程式中，我們使用嚴格單調遞增，所以高度一樣的話我們一樣不放進 stack 中，另外我們的 stack 同時存儲 hist 的高度以及 index，這樣在算面積時比較快。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def largestRectangleArea(self, heights: List[int]) -> int:
    
    heights.append(0)
    stack = [(-1, -1)]
    res = 0

    for i, h in enumerate(heights):
        t_i = i
        while h < stack[-1][1]:
            t_i, t_h = stack.pop()
            res = max(res, t_h*(i-t_i))

        if h > stack[-1][1]:
            stack.append((t_i, h))

    return res

85. Maximal Rectangle

Maximal Rectangle

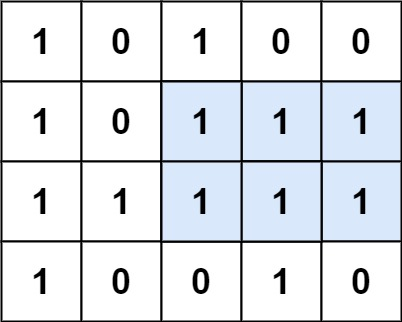
上一題的延伸題，先將 matrix 中的每個 row 轉換為對應的直方圖，接著用同樣的方式去求出直方圖的最大長方形面積就行了，以上圖來說：

  • matrix[0] = [1, 0, 1, 0, 0]
  • matrix[1] = [2, 0, 2, 1, 1]
  • matrix[2] = [3, 1, 3, 2, 2]
  • matrix[3] = [4, 0, 0, 3, 0]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def maximalRectangle(self, matrix: List[List[str]]) -> int:
    '''
    Apply monotonic stack to calculate maximal rectangle
    1. reserve one more space for the zero
    2. put a negative hist in the bottom to stay in a valid state (in while loop)
    3. append a zero to calculate remaining hist in stack
    '''

    n = len(matrix)
    m = len(matrix[0])+1    # 1
    heights = [0]*m
    res = 0

    for i in range(n):
        stack = [(-1, -1)]  # 2
        matrix[i].append(0) # 3

        for j in range(m):
            heights[j] = heights[j]+1 if matrix[i][j] == '1' else 0

            t_j = j
            while heights[j] < stack[-1][1]:
                t_j, t_h = stack.pop()
                res = max(res, t_h*(j-t_j))

            if heights[j] > stack[-1][1]:
                stack.append((t_j, heights[j]))

    return res