介紹

介數中心性（Betweenness Centrality）是社會網絡分析中常用的一種指標，用於度量一個節點在整個網絡中扮演了多重要的角色，簡單來說，介數中心性指標評估了一個節點在網絡中擔任了多少條最短路徑的中介者角色。

更白話一點，介數中心性看的是一個節點有多常被其他人經過，舉例來說：某些公車站點連接了不同的公車路線，這些公車站點對於連接整個公車網絡起著重要的作用，如果這些公車站發生了任何問題，整個公車路線都會受到影響。這些公車站點就是具有高介數中心性的節點。

計算方法

介數中心性

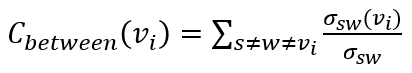
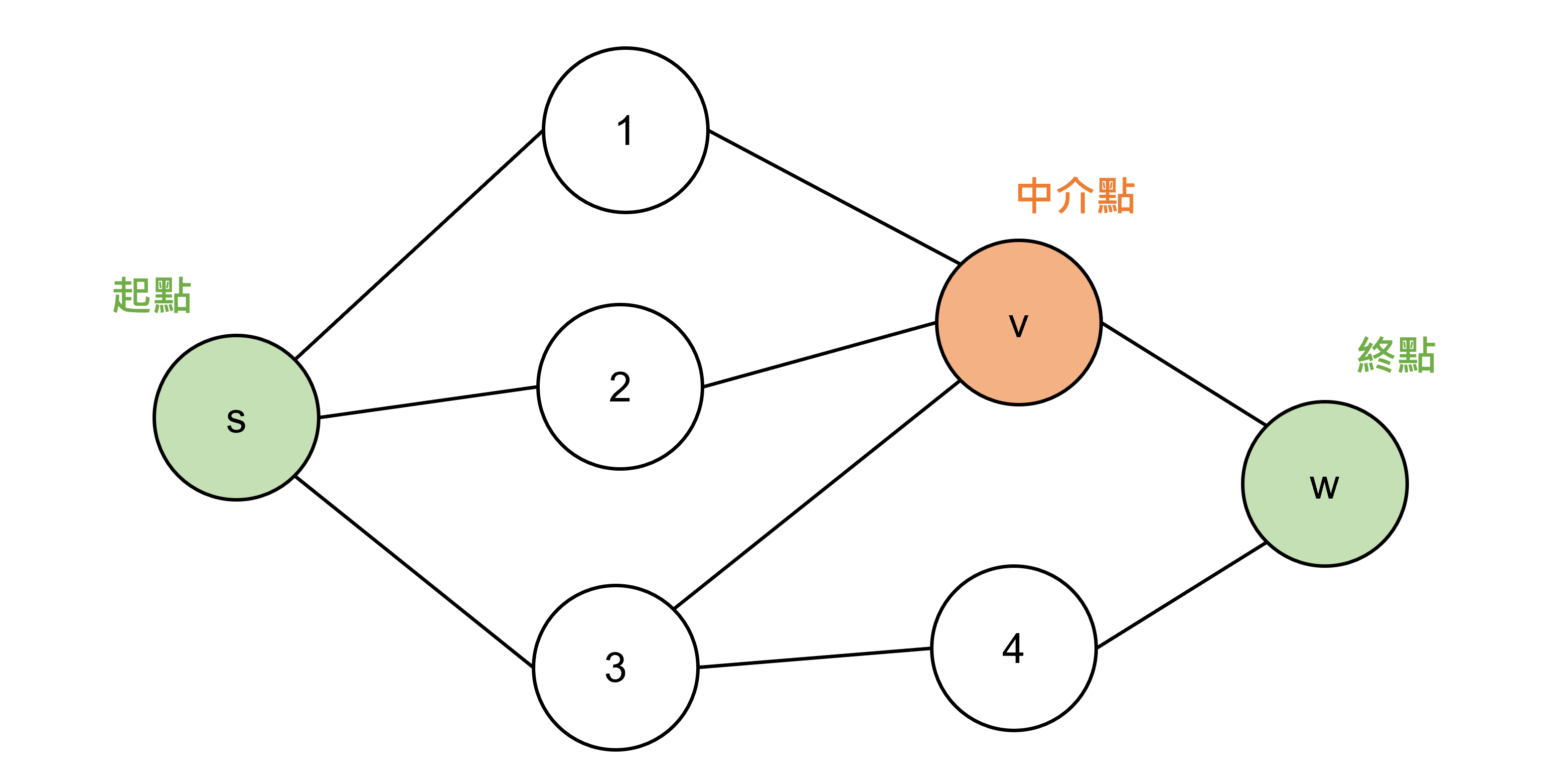
公式中，𝜎(sigma)表示最短路徑的數量，分母的意思是從點s到點w的最短路徑的數量，分子的意思是從點s到點w的最短路徑中經過v點的數量，聽起來有點抽象，我們用下面這張圖來解釋：

從s點到w點的最短路徑總共有4條，分別是
s -> 1 -> v -> w
s -> 2 -> v -> w
s -> 3 -> v -> w
s -> 3 -> 4 -> w
所以分母就是4，其中經過v的有三條所以分子就是3，能算出在s到w的路徑中，v的介數中心性就是3/4。
但要注意的是網絡中的任一點都有可能是s或是w，因此若要計算整個網絡當中v的中心性，我們要將網絡中的所有組合加總(Σ)才能得到最後的結果。

標準化

聰明的你可能會發現網絡中的節點越多，算出來的值也越大(因為是加總)，因此，為了讓不同網絡之間能被拿來比較，我們要對其進行標準化。

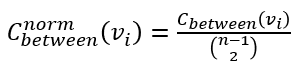
其中，分母是Binomial Coefficient，指的是一個網絡的最大可能介數中心性(網路中任選兩點、n-1取2)：

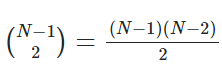
(上面標準化公式的假設是網絡是沒有方向性的，如果有方向性的話就不用除2了。)

Python 實作

網路上很多有關Betweenness Centrality的教學都是直接套networkx套件，但對於程式邏輯究竟如何實現卻是著墨很少，因此接下來要以不用套件的方式來實現unweighted graph中Betweenness Centrality的計算！

在開始實作前，我們要先把 unweighted graph 轉換成以下格式：

1
2
3
4
5

graph = {
    0 : [1, 2, 3], # 節點 : [他的鄰居]
    1 : [0, 4],
    ...
}

Pseudo Code

來看看Pseudo Code，這個算法可以計算出graph中各個點的Betweenness Centrality:

程式邏輯

看了霧煞煞? 沒關係，來解釋一下變數的意涵：

s: 起點
v: 中介點
w: 終點
S: stack，後進先出的佇列，用來儲存已經遍歷過的節點
P: path，s到w的最短路徑中，所經過的鄰居v
σ: sigma，s到其他點的最短路徑的數量
d: distance，s到其他點的最短距離
Q: queue，先進先出的佇列，用來實現BFS
δ: delta，介數中心性 (單一個節點s的結果)
C: centrality，介數中心性 (sum of delta)

程式邏輯其實很簡單，先初始化graph的共用的變數(C)，接著就是對每個節點(for s in graph:)做下面三個步驟：

1. 初始化變量

1
2
3
4
5
6
7

S = [] # stack
P = {node: [] for node in graph} # path
sigma = {node: 0 for node in graph} # 初始化為-1，因為原點是0
sigma[s] = 1 
d = {node: -1 for node in graph} # distance
d[s] = 0
Q = deque([s]) # queue

• 這部分就是根據各個變量的性質去初始化而已，唯一需要注意的是距離(d)一開始要初始化為-1，因為原點會是0。

2. 計算最短路徑 (BFS)

1
2
3
4
5
6
7
8
9
10
11

while Q:
    v = Q.popleft()
    S.append(v)
    for w in graph[v]: # for neighbor in neighbors
        if d[w] < 0: # 如果遇到新的節點才去更新他的距離
            Q.append(w)
            d[w] = d[v] + 1
        # -----------------------------------------------       
        if d[w] == d[v] + 1: # 判斷v是否在s到w的最短路徑中
            sigma[w] += sigma[v] # 透過v去更新w的最短路徑數
            P[w].append(v)

• 在這段程式中，我們可以把他切成兩半，前半段是基本的BFS演算法，比較不一樣的地方在於我們將queue彈出的節點再存入stack中，紀錄所有遍歷過的點；後半段則是從w的鄰居中，去尋找鄰居v是否位於最短路徑當中(透過判斷最短距離是否相差1)，如果是的話那就透過v去更新更新w的sigma，並且將v記錄至w的path中。

3. 計算Betweenness Centrality

1
2
3
4
5
6
7
8

delta = {node: 0 for node in graph}
# -----------------------------------------------   
while S:
    w = S.pop() # 從遍歷過的節點中pop一個
    for v in P[w]:
        delta[v] += (sigma[v]/sigma[w]) * (1 + delta[w])
    if w != s:
        C[w] += delta[w]

• delta其實也是初始化變量的一部分啦，只是Pseudo Code放在這部分所以寫在這邊。
• 我們將節點從stack中取出來，去更新這些點的Betweenness Centrality，之所以用stack有兩個原因，第一個原因是我們只需要考慮能到達的節點，第二個原因是我們希望由終點往起點去更新。
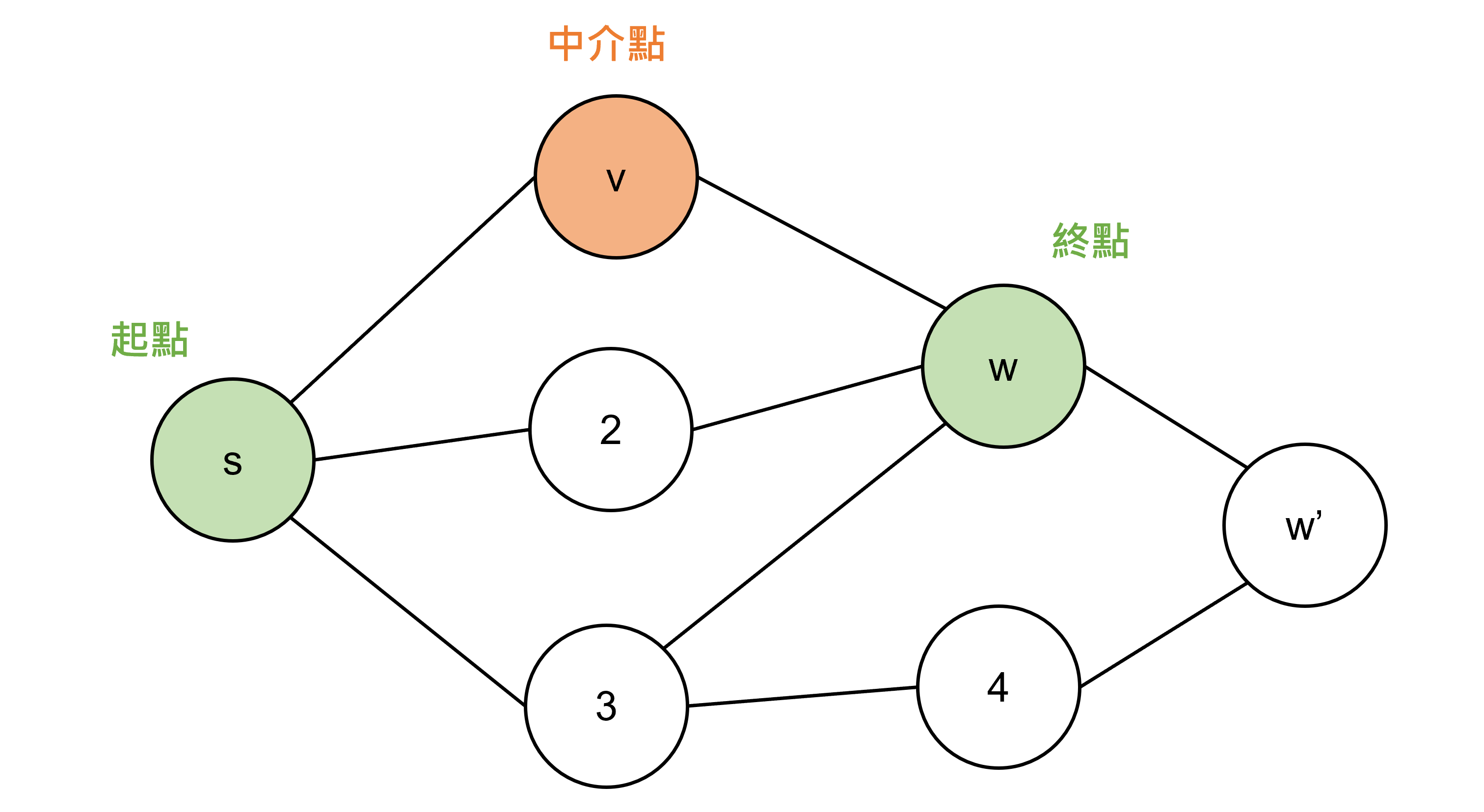
• 接著我們將每個w的path中的v取出，去更新這些v，sigma[v]/sigma[w]表示經過v的最短路徑數/經過w的最短路徑數，這邊比較讓人confused的點應該是，根據前面提到的Betweenness Centrality公式，不是只有sigma[v]/sigma[w]嗎?為什麼要乘以1+delta[w]呢?原因是目前的介數中心性只考慮了v之於w的影響，我們要對其進行修正以納入w後面的節點的影響，我們一樣拿前面用過的例子來解釋：

我們把原本的v當成新的w，把點1當成新的v，從s到w的最短路徑有三條，分別是
s -> v -> w
s -> 2 -> w
s -> 3 -> w
其中，經過v的只有一條，所以算出來Betweenness Centrality就是sigma[v]/sigma[w] = 1/3，但是!!! v不只在s -> w的最短的路徑上，他也位於s -> w'的最短路徑中，這部分也要考慮進去，前面提到從s -> w'共有4條最短路徑，經過現在的v的只有1條，因此這部分是sigma[v]/sigma[w'] = 1/4，而這個值其實會等於1/3 * 3/4，其中3/4是我們前面算得的delta[w]，因此把s -> w與s -> w'的結果加起來，就會是：
(sigma[v]/sigma[w]) + (sigma[v]/sigma[w'])
=(sigma[v]/sigma[w]) + (sigma[v]/sigma[w])*delta[w]
=(sigma[v]/sigma[w]) * (1+delta[w])

• 最後，針對非起點s的節點，我們將其更新到最終結果中。

標準化的部分雖然不在Pseudo Code中，但一般來說會順便做，方法如同公式的部分提到的，除以((n-1)*(n-2))/2就好。

1
2

for node in graph:
    C[node] /= ((n-1)*(n-2))/2

簡化版架構

1
2
3
4
5
6
7
8
9
10

def betweenness_centrality(graph):
    C = {node: 0 for node in graph}

    for s in graph:
        1. 初始化變量
        2. 計算最短路徑 (BFS)
        3. 計算centrality
    
    do Normalization
    return C

完整程式碼

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

def betweenness_centrality(graph):

    C = {node: 0 for node in graph} # centrality
    n = len(C)

    # 遍歷每個節點
    for s in graph:
        # 1. 初始化變量
        S = [] # stack
        P = {node: [] for node in graph} # path
        sigma = {node: 0 for node in graph} # 初始化為-1，因為原點是0
        sigma[s] = 1 
        d = {node: -1 for node in graph} # distance
        d[s] = 0
        Q = deque([s]) # queue
        
        # 2. 計算最短路徑 (BFS)
        while Q:
            v = Q.popleft()
            S.append(v)
            for w in graph[v]: # for neighbor in neighbors
                if d[w] < 0: # 如果遇到新的節點才去更新他的距離
                    Q.append(w)
                    d[w] = d[v] + 1
                if d[w] == d[v] + 1: # 判斷v是否在s到w的最短路徑中
                    sigma[w] += sigma[v] # 透過v去更新w的最短路徑數
                    P[w].append(v)

        # 3. 計算centrality
        delta = {node: 0 for node in graph}
        while S:
            w = S.pop() # 從遍歷過的節點中pop一個
            for v in P[w]:
                delta[v] += (sigma[v]/sigma[w]) * (1 + delta[w])
            if w != s:
                C[w] += delta[w]

    # Normalization
    for node in graph:
        C[node] /= ((n-1)*(n-2))/2 # 將每個節點除以最大可能值

    return C

結語

如果真的遇到要計算Betweenness Centrality的情況，當然還是直接用networkx套件裡的betweenness_centrality就好了啦，寫這篇單純是因為網路上都找不到有人說明算法的邏輯，所以希望寫這篇能幫助到其他想了解算法的人。
要注意上面的算法建立在所有edge的權重都是一樣的情況下，也就是點與點之間不是1就是0的binary關係，那如果每條edge有不同的權重呢?方法其實也不太意外，就是把程式中計算最短路徑的部分換掉就好了，根據實際情況可以選擇Dijkstra或是Bellman–Ford等。