Spectral Clustering - 算法解析與 numpy 程式實作

發表於 分類於 閱讀次數： 文章字數： 1.9k 所需閱讀時間 ≈ 8 分鐘

前言

Spectral Clustering

在社群網絡中分析中，有時候會想要找出網絡當中的社群(community detection)，一個最直觀的想法是直接對網絡進行分群，那麼分群結果就是各個community了。
如果我們能夠計算各個節點之間的相似性，那麼我們當然可以直接套用傳統的分群方法，如cosine similiarity，但一來是相似度特徵可能很難取得，二來是這樣分群的話就沒有利用到網絡的結構了，這時我們可以改為使用基於圖論的分群方法。
今天這篇文章會帶大家簡單瞭解什麼是cut approach, balanced-cut approach以及其代表方法spectral clustering，並示範不依賴其他套件，僅使用numpy實作spectral clustering。

大綱

內文

Mini-cut Approach

Cut approach，顧名思義是將網絡給切開來形成多個網絡，屬於partitional clustering的一種，每個節點只會屬於一個community，並且community之間也不會overlapping，而Mini-cut Approach則是希望在切割網絡時能最小化切掉的edge數量。
聽起來很直觀，但這樣切會有一個問題，那就是有可能會切出一些非常小的community，導致分群不夠balance。

Balanced-cut Approach

為了解決Mini-cut Approach的缺點，Balanced-cut Approach在切割網絡時除了考量原本的edge，另外除以community的node數做加權調整，切割的目標從最小化edge數轉為最小化ratio cut，公式如下:
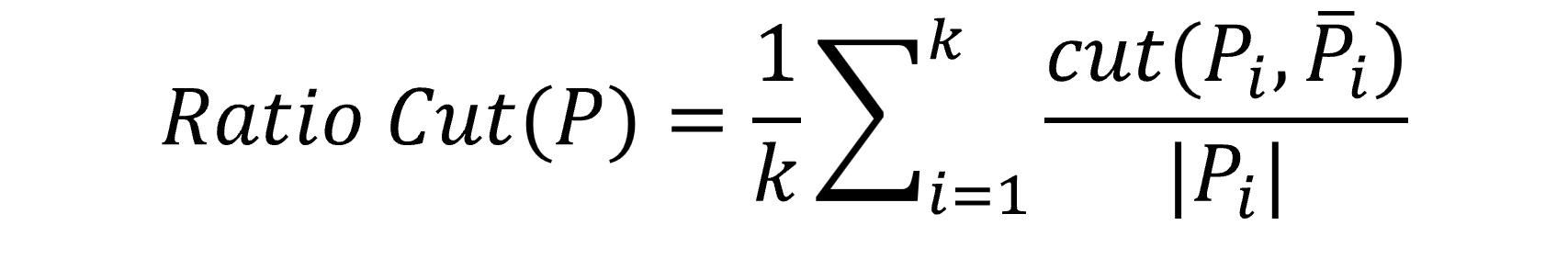
Ratio Cut formula

公式解釋: 分成k群(k要自己決定)，每次取一個群Pi出來看，分子部分表示將Pi切開的話會切到的edge數，分母部分表示Pi內部的node數，將k個群的結果加總起來就會是整個網路的ratio cut分數。

Matrixs

為了要計算Ratio Cut，我們先要來認識一下三種矩陣:

  1. Diagonal Degree Matrix 度數矩陣
    Degree(度數)指的是一個node有多少個鄰居，將這些Degree轉換為對角矩陣(Diagonal Matrix)就得到Diagonal Degree Matrix。
1
2
3
4
5
6
7
8
D = np.array([
  [2, 0, 0, 0, 0, 0, 0],
  [0, 4, 0, 0, 0, 0, 0],
  [0, 0, 2, 0, 0, 0, 0],
  [0, 0, 0, 3, 0, 0, 0],
  [0, 0, 0, 0, 2, 0, 0],
  [0, 0, 0, 0, 0, 3, 0],
  [0, 0, 0, 0, 0, 0, 2]])
  1. Adjacency Matrix 鄰接矩陣
    只要是對Graph有些概念的人應該都對Adjacency Matrix不太陌生，Adjacency Matrix描述了node之間的關係，下面例子假設node之間的關係都是雙向的，所以會是個對稱矩陣。
1
2
3
4
5
6
7
8
A = np.array([
  [0, 1, 0, 0, 1, 0, 0],
  [1, 0, 1, 1, 0, 0, 1],
  [0, 1, 0, 1, 0, 0, 0],
  [0, 1, 1, 0, 0, 1, 0],
  [1, 0, 0, 0, 0, 1, 0],
  [0, 0, 0, 1, 1, 0, 1],
  [0, 1, 0, 0, 0, 1, 0]])
  1. Laplacian Matrix 調和矩陣(拉普拉斯矩陣)
    Laplacian Matrix 的算法就是直接將Diagonal Degree Matrix 減去 Adjacency Matrix，聽起來可能讓人滿頭問號，為什麼要這麼做? 這邊先賣個關子，繼續看下去就知道了。
1
2
3
4
5
6
7
8
L = np.array([
  [ 2, -1,  0,  0, -1,  0,  0],
  [-1,  4, -1, -1,  0,  0, -1],
  [ 0, -1,  2, -1,  0,  0,  0],
  [ 0, -1, -1,  3,  0, -1,  0],
  [-1,  0,  0,  0,  2, -1,  0],
  [ 0,  0,  0, -1, -1,  3, -1],
  [ 0, -1,  0,  0,  0, -1,  2]])

Calculation

現在先假設我們已經知道分群的結果了，並將結果以0,1的形式表示為一個matrix，令這個結果為X，下面結果是我隨便分的，分3群，X[i][j]==1表示nodei屬於clusterj。

1
2
3
4
5
6
7
8
X = np.array([
  [1, 0, 0],
  [1, 0, 0],
  [0, 0, 1],
  [0, 0, 1],
  [0, 1, 0],
  [0, 1, 0],
  [0, 1, 0]])
  1. Diagonal Degree Matrix 解釋
    我們先將X的轉置矩陣與D做內積(X.T.dot(D)):
1
2
3
array([[2, 4, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 2, 3, 2],
       [0, 0, 2, 3, 0, 0, 0]])

觀察一下結果會發現，這個矩陣就只是是把Degree填到對應的cluster中而已。
接著我們再把上面結果與X做內積(X.T.dot(D).dot(X)):

1
2
3
array([[6, 0, 0],
       [0, 7, 0],
       [0, 0, 5]])

這個結果其實就表示每個cluster的degree總和。

  1. Adjacency Matrix 解釋
    接著我們直接將上面公式的D換成A(X.T.dot(A).dot(X)):
1
2
3
array([[2, 2, 2],
       [2, 4, 1],
       [2, 1, 2]])

會發現結果表示在cluster與cluster間互相連接的edge數。

  1. Laplacian Matrix 解釋
    如果我們將兩個結果相減的話，會發現每一行的第i個元素(對角)就是我們想要計算的cut數(分子部分)!!!
1
2
3
array([[ 4, -2, -2],  # i=0, 4
       [-2,  3, -1],  # i=1, 3
       [-2, -1,  3]]) # i=2, 3

接著我們另外計算每個cluster裡面共有多少個node，我們可以將X的轉置後與自己相乘(X.T.dot(X)):

1
2
3
array([[2, 0, 0],
       [0, 3, 0],
       [0, 0, 2]])

最後將對角的結果相除後加起來就是算平均就得到Ratio Cut的分數啦~~~
(我這邊直接矩陣相除，大家可以自己算。)

1
2
3
array([[ 2. , -inf, -inf],
       [-inf,  1. , -inf],
       [-inf, -inf,  1.5]])

根據上面矩陣運算的過程，我們能將公式重新整理為:
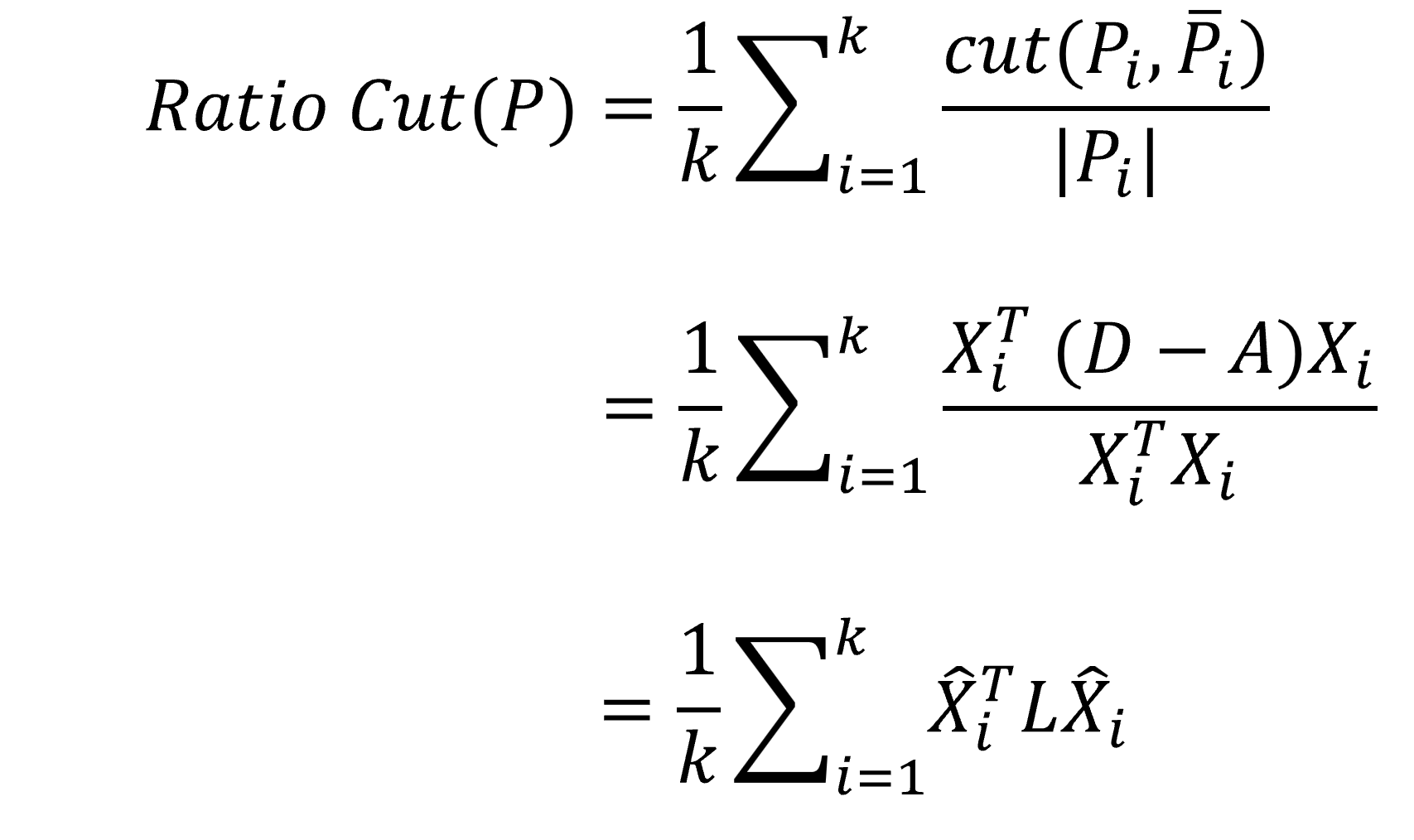
ratio cut formula extended

在第三行的部分，我們另外對X進行標準化(同除以分母)變成了X prime。

Minimize

回到最一開始的問題，我們的目標是要最小化ratio cut的分數，方法就是透過上面的公式去求解X prime矩陣，難過的是，還記的X矩陣裡最一開始只能填入0跟1嗎，想要在這樣嚴格的限制下求出最佳解是個NP-hard的問題。
不過不要灰心，我們還是可以放寬條件，套用近似演算法，其中一種方法就是接下來要介紹的Spectral Clustering~~~

Spectral Clustering

Spectral Clustering 基於ratio cut，不過X矩陣中可以填入的值變成介於0~1之間，在放寬條件後，這個最小化問題的解可以被證明是求解Laplacian Matrix的前k小個特徵值的特徵向量。

  1. Eigenvalue & Eigenvactors
    我們可以用np.linalg.eig來替我們計算特徵值與特徵向量，並使用np.argsort來替我們找出最小的k個特徵向量。
1
2
3
4
5
6
7
# calculate eigenvalue and eigenvector
eig_value, eig_vector = np.linalg.eig(L)

# get eigenvector with smallest eigenvalue
k = 3
top_k = np.argsort(eig_value)[:k]
top_k_vector = eig_vector[:, top_k]

得到的結果如下:

1
2
3
4
5
6
7
array([[ 0.37796447, -0.45244521, -0.41243936],
       [ 0.37796447,  0.17351892, -0.08541899],
       [ 0.37796447,  0.54280925, -0.41243936],
       [ 0.37796447,  0.32598548, -0.08541899],
       [ 0.37796447, -0.58986844, -0.08541899],
       [ 0.37796447, -0.09036404,  0.37705765],
       [ 0.37796447,  0.09036404,  0.70407803]])
  1. K-means
    由於得到的特徵值並無法直接拿來做解釋，因此Spectral Clustering另外使用了K-means來為這些特徵值做分群，因為最小的特徵值為0、特徵向量一定是常數，所以我們可以把它刪去，也就是說，如果我們想要分成k群，那我們至少需要使用k-1個特徵向量。
    下面程式提供一個簡單的K-means範例，可以根據自己的需求另外設置停止條件。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def k_means(X, k, max_iters=10000):
    # randomly initialize centroids
    centroids = X[np.random.choice(len(X), k, replace=False)]
    for _ in range(max_iters):
       # calculate distances
       distances = np.linalg.norm(X[:, np.newaxis] - centroids, axis=2)
       # assign labels 
       labels = np.argmin(distances, axis=1)
       # calculate new centroids
       centroids = np.array([np.mean(X[labels == i], axis=0) for i in range(k)])
    return labels

# remove first vector
features = top_k_vector[:, 1:]
# do k-maens
labels = k_means(features, k)

這樣就得到分群結果啦~~~(注意: 實際執行數字的順序可能不一樣)

1
array([2, 0, 0, 0, 2, 1, 1], dtype=int64)

結語

其實忽略到複雜的數學證明的話，Spectral Clustering的概念還挺直觀的，文章參考了台大資管系的陳建錦教授所使用的上課講義，經過本人吸收轉化撰寫而成。