Python 隨便寫 - 用牛頓法 (Newton's method) 計算內部報酬率 (IRR)

發表於 分類於 閱讀次數： 文章字數： 650 所需閱讀時間 ≈ 3 分鐘

內部報酬率 (Internal Rate of Return，IRR)

內部報酬率是一種用來衡量投資效益的指標，其概念是計算出一個折現率，使淨資金流入的現值與淨資金流出的現值加總為 0，也就是淨現值為 0 (NPV=0)。

淨現值的數學公式如下:

NPV=∑t=0NCt(1+r)t{NPV = \displaystyle \sum _{t=0}^{N}{\frac {C_{t}}{\left(1+r\right)^{t}}}}

其中 r{r} 是折現率、N{N} 為期間、Ct{C_{t}} 為第 t{t} 年的淨現金流量。
當我們帶入一個 r{r} 能使得 NPV=0 時，我們就把這個 r{r} 稱 IRR。

一般來說我們可以使用插值法來計算 IRR，假設 r{r}=5% 時 NPV > 0，r{r}=6% 時 NPV < 0，那我們就能說 IRR 在 5%~6% 之間，可以用 Binary Search 的概念去實作，但這次我決定用點不一樣的。

牛頓法 (Newton’s method)

所謂的牛頓法是一種求解方程式 f(x)=0{f(x) = 0} 的根的方法。我們把上面 NPV 公式裡的 r{r} 換成 x{x}，便可以把 NPV 視作 f(x){f(x)} ，則 IRR 即是 f(x)=0{f(x) = 0} 的根，因此牛頓法正好可以拿來求解 IRR。

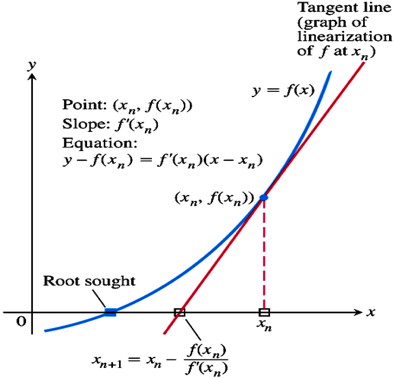
Newton method

我們讓 f(x){f(x)} 對 xn{x_{n}} 做偏微分得到一斜率，進一步計算出通過 xn{x_{n}} 之切線，接著找到切線與 x 軸的交點 xn+1{x_{n+1}}，其值為:

xn+1=xn−f(xn)f′(xn){\displaystyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}}

能發現 xn+1{x_{n+1}} 相比於 xn{x_{n}} 更靠近我們要求的根，因此我們能迭代的進行這個操作，直到 f(xn)=0{f(x_{n}) = 0}，或者 abs(f(xn)−0)<tolerance{abs({f(x_{n})} - 0) < tolerance}。

Python 程式碼

首先是計算 NPV 的部分，這邊為了因應現金流不固定的情況所以會先計算每一期的 time_diff：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from datetime import datetime

def npv_with_dates(cashflows, rate):
    """
    Calculate NPV (with date)
    :param cashflows: [(date 1, cash 1), (date 2, cash 2) ...]
    :param rate: discount rate
    :return: NPV
    """
    npv = 0
    for date, cashflow in cashflows:
        time_diff = (date - cashflows[0][0]).days / 365.0
        npv += cashflow / ((1 + rate) ** time_diff)
    return npv

接著就是牛頓法的部分，給定一個初始的折現率開始迭代優化，derivative 是偏微分的結果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def irr_with_dates(cashflows, initial_rate=0.1, tolerance=1.0e-6, max_iter=100):
    """
    Calculate IRR with Newton's method (with date)
    :param cashflows: [(date 1, cash 1), (date 2, cash 2) ...]
    :param initial_rate: initial discount rate
    :param tolerance
    :param max_iter: max iterations
    :return: IRR
    """
    rate = initial_rate
    for _ in range(max_iter):
        npv = npv_with_dates(cashflows, rate)
        derivative = 0
        for date, cashflow in cashflows:
            time_diff = (date - cashflows[0][0]).days / 365.0
            derivative += -time_diff * cashflow / ((1 + rate) ** (time_diff + 1))
        rate -= npv / derivative
        if abs(npv) < tolerance:
            return rate
    return None

執行程式碼：

1
2
3
4
cashflows = [(datetime(2023, 1, 1), -100), (datetime(2023, 5, 1), 20), (datetime(2023, 9, 1), -10), (datetime(2024, 1, 1), 50), (datetime(2024, 3, 1), 70)]
irr_value = irr_with_dates(cashflows)
print(f"IRR: {irr_value*100:.2f} %")
# IRR: 29.98 %

參考資料

牛頓法 ( Newton’s Method )